Assigning Subjects to Groups in a Controlled Trial Will G Sportscience 14, 7-12, 2010 (sportsci.org/2010/wghminim.htm) Sport and Recreation, AUT University,
Auckland 0627, New Zealand. Email. Reviewer:
Alan M Batterham, School of Health and Social Care, University of Teesside,
Middlesbrough TS1 3BA, UK. |
|
When practicable, the controlled trial is the best design to establish the efficacy of treatments or other interventions and the direction of causality between inter-related variables (Hopkins, 2008). The superiority over other designs arises from having a treatment or intervention group and a control or other reference group that differ ideally in only one respect, the applied treatment. The difference between the effects in the two groups is therefore the pure effect of the treatment. Randomization was long considered the best way to allocate subjects to the treatment and control groups, but it is now apparent that non-random allocation aimed specifically at minimizing differences in group means of subject characteristics is superior (Scott et al., 2002). Software is available for such allocation in the kind of clinical trial where each subject is allocated immediately on recruitment (e.g., Evans et al., 2004). However, many clinical and non-clinical trials offer the opportunity to enhance minimization by allocation after all subjects have been recruited, and I have been unable to find software for this approach. In this article I explain the basis of randomization and minimization, I explain why subject characteristics should be included in the analysis as covariates regardless of the method of allocation, and I provide spreadsheets for allocation based on minimization during and after subject recruitment. In a randomized controlled trial subjects are allocated to groups in a random fashion, with the aim of making each group sample representative of the population. When this aim is fulfilled, the effect of the treatment in each group can be assumed to apply to the population generally, apart from the usual sampling uncertainty that is dealt with using confidence limits or other inferential statistics. One way in which the aim is not fulfilled occurs when the mean value of a subject characteristic in a group differs from the population mean (e.g., the group is heavier than the population average). If the effect of the treatment depends on the subject characteristic (e.g., greater reduction in blood cholesterol in heavier overweight subjects), the mean effect of the treatment in the group will differ substantially from the mean effect in the population. The resulting error in the estimate of the effect of the treatment depends on what happens in the comparison group.
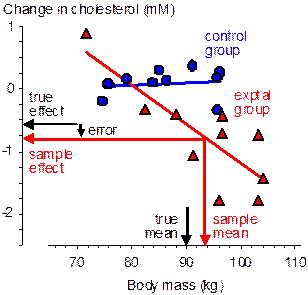
At one extreme, the subject characteristic has no effect on the reference treatment (e.g., Figure 1), a possible scenario when the reference treatment is an ineffective placebo or low-dose treatment. The inaccuracy in the estimate of the effect will therefore depend only on the difference between the population and active-treatment means of the characteristic. With randomized allocation the typical difference between these means is the standard error of the active-treatment mean, SD/√n, where SD is the standard deviation of the characteristic in the population and n is the group sample size. In standardized units, the typical difference is therefore simply 1/√n. When n is <25, the standardized difference between the sample and population means is therefore typically >0.20, the widely accepted default for smallest important differences. I will discuss shortly whether this difference will have a substantial effect on the outcome. Meanwhile consider the typical difference between the means with allocation by minimization (not shown in the figure). If minimization is perfect, there is no difference between the group means of the subject characteristic, so the typical difference of a group mean from the population mean is given by the standard error of the mean of a sample of size 2n with two groups, 3n with three groups, and so on. Thus, the standardized difference between a group mean and the population mean is substantial only when the sample size in each group is <25/2 with two groups, <25/3 with three groups, and so on. Minimization clearly allows for smaller sample sizes but does not eliminate the error arising from the sample mean being different from the population mean.
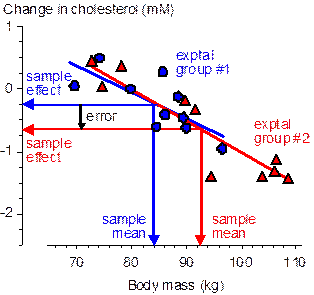
Now consider the outcome at another extreme, when the subject characteristic has the same effect on the active and comparison treatments (e.g., Figure 2), a possible scenario when two active treatments are compared. With randomization the inaccuracy depends on the typical difference in the means of the two groups, which is therefore √2.SD/√n (because the groups are independent and each has the same standard error of the mean, SD/√n). The standardized difference is therefore √(2/n), which is >0.20 when n is <50. Perfect minimization, on the other hand, results in no difference between the means and therefore completely eliminates the effect of the subject characteristic (not shown in the figure). Some controlled trials are more susceptible than others to errors arising from different group means of subject characteristics. The worst design in this respect is the post-only parallel groups, where the dependent variable is measured once only, after the treatment. This kind of design is required if the outcome is a new event (e.g., illness, death) or a count of new events (e.g., injuries, wins), although it can also be used for continuous dependent variables–see the article on a controlled-trial decision tree for more (Batterham and Hopkins, 2005a). It is not unusual to have a substantial correlation between a characteristic and the dependent variable, and this correlation multiplied by the standardized group mean difference becomes the error in the treatment effect (because DY/SDY = r.DX/SDX, where Y is the dependent variable, X is the subject characteristic, and r is the correlation coefficient). This kind of design ideally requires hundreds of subjects, which automatically reduces the impact of subject characteristics to a trivial level when allocation is by randomization. Minimization is nevertheless advisable, especially if the analysis involves comparisons of subgroups with less than the optimal numbers of subjects. In the more common pre-post parallel-groups design (the kind exemplified by the data in Figures 1 and 2), there has to be a sufficiently large correlation between the characteristic and the change score of the dependent variable for the error to be appreciable. Such correlations are likely to be less frequent than those between the characteristic and the raw score of the dependent, but in general there is no way of knowing at the design stage whether there is such a correlation. Minimization is therefore still advisable. The controlled trials with the smallest errors arising from group-mean subject characteristics are crossovers, because there would have to be an interaction between the subject characteristic and any order effect in the efficacy of the treatment. On the other hand, sample sizes with a post-only crossover can be much smaller than those in the pre-post parallel-groups design (down to one quarter as many), so the differences between group means will be typically greater. Once again, minimization when allocating subjects to groups (here, those defined by the order of treatments) is a sensible precaution. I have used the term error and avoided bias thus far when referring to the effect of imbalance in subject characteristics on a treatment effect. Bias would be appropriate if the effect turned up on average as an over-estimate or under-estimate, but differences in group means of subject characteristics arising from random allocation of subjects must be zero on average; the error arising from differences in group means therefore must also be zero on average. In other words, subject characteristics may modify the effect of a treatment, but if you haven't measured them, they can't be said to bias the outcome. Once a subject characteristic is measured and found to have different group mean values, it is perhaps acceptable to state that the particular effect of the treatment you observed could be biased by the particular difference in the means of the subject characteristic. You could also state that the effect of the treatment could be confounded by the characteristic, but arguably bias and confounding should be used when a method of subject allocation produces only consistent differences in group means. A more important technical point relates to inferences about differences in group-mean characteristics. As I pointed out in my article on controlled trials (Hopkins, 2006), the impact of the difference you observe is what matters, and it does not make sense to calculate the confidence interval or p value for the differences. Evaluate the magnitude of the difference using standardization, but do not assert whether the difference is clear or statistically significant. While it should now be obvious that minimization of differences in group means of characteristics can result in better precision in the estimate of a treatment effect, it is less obvious that the calculated width of the confidence interval is on average the same as that with randomization when the analysis does not account for the differences in means. Decisions about the clinical, practical, mechanistic or statistical significance of an effect are based on the width of the confidence interval or on the underlying probability distribution of the true value of the effect (Batterham and Hopkins, 2005b; Hopkins, 2007a), so better precision with minimization has to be apparent as a narrower confidence interval for minimization to be worth the effort. One way to take the effect of subject characteristics into account is to include them as covariates in the analysis. Without minimization, inclusion of a covariate adjusts away the error arising from differences in the means (or in the case of the outcome in Figure 1, the analysis reduces the effect of the difference between the group and population means). Inclusion of a covariate also improves precision by accounting for the otherwise unexplained variance associated with the covariate. With minimization there is the same gain in precision from accounting for unexplained variance, but because there is little or no difference in group means, the adjustment for the difference involves little or no extrapolation with the linear covariate term. Precision is therefore overtly a little better following adjustment with minimization than with randomization; more importantly, the adjusted estimate is less sensitive to violation of the assumption of linearity of the effect of the covariate. Another way to account for minimization in the analysis is available when assignment is performed after all subjects have been recruited. The spreadsheet I have devised for such assignment gives primary importance to minimizing differences between the means of one characteristic, first by ranking the subjects on this characteristic, then by assigning each subject in a cluster of contiguous subjects to each group. This process effectively makes each cluster of values into those of a single subject (the cluster) with repeated measurement (the values with the different treatments within the cluster). An analysis that takes this extra level of repeated measurement into account produces narrower confidence intervals than the usual analysis: in essence, the confidence interval for the difference in the effect of the treatment between groups should be based on the paired t statistic rather than the unpaired t statistic. My spreadsheet for analysis of pre-post crossovers (Hopkins, 2006) will perform such comparisons, as will appropriate mixed modeling and repeated-measures ANOVA. In pre-post parallel-groups studies with assignment after recruitment, the most important characteristic to minimize should almost invariably be the baseline value of the dependent variable. If the random error in this variable is an appreciable proportion of between subject differences (that is, the variable has moderate to low reliability), the baseline values have a substantial artifactual negative correlation with the change scores known as regression to the mean. Minimizing this characteristic eliminates the error arising from regression to the mean; analyzing with the paired t statistic or a mixed model reveals the narrower confidence interval; and including the baseline value as a covariate reveals any real effect of the baseline on the effect on the treatment. The gain in precision depends on the error of measurement relative to the true (error-free) between-subject SD at baseline: if the error is large (i.e., the dependent variable is very unreliable), the confidence interval is narrower by a factor of 1/√2 (=0.71); if the error is small, there is no gain in precision. I performed simulations analyzed with mixed modeling in a SAS program to check these assertions in the special case of a dependent variable with no real differences between subjects in the baseline test (which gives the most regression to the mean) and with minimization of the baseline means in two groups. Analysis of the Type 0 error for the eight different kinds of analysis showed that the confidence intervals were either accurate, a little conservative (too wide), or very conservative (in the case of minimization followed by analysis without pairing or adjusting). I got similar results with simulations using a spreadsheet to generate the data and my controlled-trial spreadsheets for the analyses, although I did find that the pre-post crossover spreadsheet produced confidence intervals that were too narrow in the case of minimized groups with the baseline included as a covariate. I presume this result indicates a failure of least-squares estimation but not restricted maximum likelihood (the basis of mixed modeling) in this special case, arising from violation of the assumption of independence. See below for links to the SAS simulations and to the spreadsheet simulations. Finally, some details on how my minimization spreadsheets work... I have already mentioned that I use the rank of the most important subject characteristic as the basis of the spreadsheet for allocation after all subjects have been recruited. The ranking is achieved using the Sort operation in Excel. The spreadsheet prompts the user to assign each subject within a cluster to the group that minimizes standardized differences between the means of the developing groups. Assignment of a cluster of subjects alternates between each end of the sorted list of subjects and gradually moves towards the center, a strategy I found to be more effective than assigning progressively from one end of the sorted data. The spreadsheet minimizes means of up to six numeric characteristics in up to five groups. Nominal characteristics representing sex (male vs female) or the presence or absence of a characteristic (e.g., sedentary vs active) are coded as 0 or 1, and for the purpose of minimizing standardized differences these characteristics are treated as if they are continuous. Nominal variables with three or more levels (e.g., SPORT with levels cycle, run, swim) need to be coded using two or more of the six variables as binary variables. The method is explained in the spreadsheets. Note that if estimation of the effects for each sex or for each level of the nominal variable is a priority, it is preferable to pre-sort subjects by sex or by the levels of the nominal variable, then perform separate assignments for each sex or level. The spreadsheet for assigning subjects as they are recruited also works by minimizing standardized differences, but ranking by any characteristic is, of course, impossible; thus all characteristics are given equal importance. To give one characteristic (e.g., baseline values of the dependent variable) twice as much importance as the other characteristics, include its values as two variables with identical values. Other minimization software is based on dichotomizing each characteristic (e.g., age becomes young and old) and then assigning each subject to the group with the smallest total of characteristics that are the same as the subject's characteristics. For more details see Altman and Bland (2005). My method is superior in principle, especially when covariates are analyzed as continuous variables, but I suspect that any differences in outcome between the various methods will be trivial. Each spreadsheet includes a panel that simulates values of subject characteristics to help the user to learn how to use the spreadsheet and to allow me to check that it performed adequately, which I have done with various sample sizes, numbers of characteristics and numbers of subjects (see below). Sampling variation occasionally results in standardized differences between means that are larger than those expected by chance with randomization (values for which are shown in the summary spreadsheet), but on average the differences are about half those expected with randomization. With allocation after recruitment the most important characteristic is particularly well minimized. In his review of this article, Alan Batterham mentioned that the minim software program allows for minimization with unequal proportions of subjects in each group. He pointed out to me that researchers might opt for a relatively smaller proportion in a group with an aversive treatment, even though to maintain precision an overall larger sample size is required. Similarly, researchers might opt for a larger proportion in a group with a potentially beneficial treatment, if subjects are reluctant to volunteer with only a 50/50 chance of receiving that treatment. A simple way to achieve proportions of 2:1, 3:1, 4:1 and 3:2 with my spreadsheets is to assign subjects to more than two groups then merge two or more groups. Spreadsheets for Minimization
MinimizeMeansAfterRecruit.xls: use when allocating subjects to groups after recruiting
all subjects (or all subjects in each cohort).
MinimizeMeansAsRecruit.xls: use when allocating each subject to a group for
treatment as soon as the subject is recruited.
Other
Files
Spreadsheet to generate
data in Figures 1 and 2: a
slightly modified version of a spreadsheet in the article on understanding stats via simulations (Hopkins, 2007b).
Spreadsheet of results of simulations: to check effectiveness of the minimization
spreadsheets. This zip file has the slightly modified versions of the minimization
spreadsheets used to generate these data.
SAS program and listing (Word docs): simulations to check outcomes of various
kinds of analysis with random assignment and with assignment after
recruitment to minimize the baseline means of the dependent variable in a
pre-post parallel groups controlled trial.
Spreadsheet simulations (zip file): similar
to the above SAS program and listing.
The master file is GenerateAndAssignSubjects.xls. This file links to the controlled-trial spreadsheets,
which you should open first but not modify.
References
Altman DG, Bland JM (2005). Treatment allocation by minimisation. British Medical Journal 330, 843 Batterham AM, Hopkins WG (2005a). A decision tree for controlled trials. Sportscience 9, 33-39 Batterham AM, Hopkins WG (2005b). Making meaningful inferences about magnitudes. Sportscience 9, 6-13 Evans S, Royston P, Day S (2004). Minim: allocation by minimisation in clinical trials. http://www-users.york.ac.uk/~mb55/guide/minim.htm Hopkins WG (2006). Spreadsheets for analysis of controlled trials, with adjustment for a subject characteristic. Sportscience 10, 46-50 Hopkins WG (2007a). A spreadsheet for deriving a confidence interval, mechanistic inference and clinical inference from a p value. Sportscience 11, 16-20 Hopkins WG (2007b). Understanding statistics by using spreadsheets to generate and analyze samples. Sportscience 11, 23-36 Hopkins WG (2008). Research designs: choosing and fine-tuning a design for your study. Sportscience 12, 12-21 Scott NW, McPherson GC, Ramsay CR, Campbell MK (2002). The method of minimization for allocation to clinical trials. a review. Controlled Clinical Trials 23, 662-674 Published May
2010 |